You need to be a little careful in your thinking about this and in the terminology you use to describe the situation.
In a two-terminal linear circuit that can be modeled by a constant supply voltage source (Vs) and a constant source impedance (Rs), the maximum power dissipation will occur when the two terminals are shorted. That power dissipation will be
max power = (Vs)^2/Rs
All of this power is dissipated in the source impedance, often not very useful. (This can be very useful in certain situations where load power dissipation above some maximum may cause fire or explosion or other ill effects.)
Occasionally, we are interested in transferring maximum power from the source to the load impedance (Rl). This can be the case, for example, when the load is an antenna for radio transmission. When the load impedance is linear, the equation that models the load power can be written as
load power = (Vs/(Rs+Rl))^2*Rl = Vs^2*Rl/(Rs+Rl)^2)
Inspection of this equation will reveal that when Rl=0, load power = 0. The load power also approaches zero as the load impedance goes to infinity. Between those extremes, there is a maximum. We can find that point by differentiating this expression with respect to Rl
d(load power)/dRl = Vs^2*(Rs-Rl)/(Rs+Rl)^3
This will be zero when Rs=Rl. Thus maximum load power will be dissipated when load impedance = source impedance. It is worth noting that an equal amount of power is being dissipated by the source impedance.
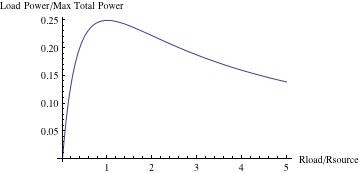Under conditions of maximum load power, the current being supplied is half the maximum current available from the source. It is neither maximum nor minimum. The circuit current is given by
current = Vs/(Rs+Rl)
Clearly, this will be maximum when Rl=0
max current = Vs/(Rs+0) = Vs/Rs At max load power conditions (Rl=Rs), this will be
max load power current = Vs/(Rs+Rs) = Vs/(2*Rs) = (1/2)*(max current)
The math above applies to linear DC circuits or to linear AC circuits when impedances are all real (with no reactive components). When the source impedance contains a reactive component (as AC impedances often do), the maximum power is transferred to a load that is the complex conjugate of the source impedance.
In AC power transmission, we are not interested in losing half the generated power in the transmission system. Rather, we want the largest possible fraction of total power to be used by the load. In that case, transformers are used to make the apparent load impedance as large as possible, so the source impedance represents a negligibly small fraction of the total circuit impedance.
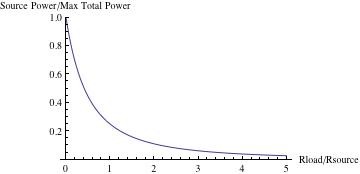
This curve shows how power dissipation in the source impedance (Rs) goes down as load impedance goes up. As stated at the beginning, maximum total power dissipation occurs when the load is zero.
In a two-terminal linear circuit that can be modeled by a constant supply voltage source (Vs) and a constant source impedance (Rs), the maximum power dissipation will occur when the two terminals are shorted. That power dissipation will be
max power = (Vs)^2/Rs
All of this power is dissipated in the source impedance, often not very useful. (This can be very useful in certain situations where load power dissipation above some maximum may cause fire or explosion or other ill effects.)
Occasionally, we are interested in transferring maximum power from the source to the load impedance (Rl). This can be the case, for example, when the load is an antenna for radio transmission. When the load impedance is linear, the equation that models the load power can be written as
load power = (Vs/(Rs+Rl))^2*Rl = Vs^2*Rl/(Rs+Rl)^2)
Inspection of this equation will reveal that when Rl=0, load power = 0. The load power also approaches zero as the load impedance goes to infinity. Between those extremes, there is a maximum. We can find that point by differentiating this expression with respect to Rl
d(load power)/dRl = Vs^2*(Rs-Rl)/(Rs+Rl)^3
This will be zero when Rs=Rl. Thus maximum load power will be dissipated when load impedance = source impedance. It is worth noting that an equal amount of power is being dissipated by the source impedance.
current = Vs/(Rs+Rl)
Clearly, this will be maximum when Rl=0
max current = Vs/(Rs+0) = Vs/Rs At max load power conditions (Rl=Rs), this will be
max load power current = Vs/(Rs+Rs) = Vs/(2*Rs) = (1/2)*(max current)
The math above applies to linear DC circuits or to linear AC circuits when impedances are all real (with no reactive components). When the source impedance contains a reactive component (as AC impedances often do), the maximum power is transferred to a load that is the complex conjugate of the source impedance.
In AC power transmission, we are not interested in losing half the generated power in the transmission system. Rather, we want the largest possible fraction of total power to be used by the load. In that case, transformers are used to make the apparent load impedance as large as possible, so the source impedance represents a negligibly small fraction of the total circuit impedance.
This curve shows how power dissipation in the source impedance (Rs) goes down as load impedance goes up. As stated at the beginning, maximum total power dissipation occurs when the load is zero.